Xungerrrr's Blog

Transformation

Compute Graphics - Homework 4

Computer Graphics
Word count: 2.1kReading time: 9 min
2019/04/09 Share

画一个立方体，边长为4，中心位置为(0, 0, 0)

首先设定立方体的初始顶点位置和颜色。立方体的边长为4，中心位置为(0, 0, 0)，所以三个坐标轴的范围都是[-2, 2]。由于正方体有六个面，每个面由两个三角形构成，因此一共有36个点。同时，我希望用立方体表现出RGB颜色空间，x轴对应红色，y轴对应绿色，z轴对应蓝色，所以要根据点的坐标设置对应的颜色。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
float vertices[] = {
    -2.0f, -2.0f, -2.0f,  0.0f, 0.0f, 0.0f,
    2.0f, -2.0f, -2.0f,  1.0f, 0.0f, 0.0f,
    2.0f,  2.0f, -2.0f,  1.0f, 1.0f, 0.0f,
    2.0f,  2.0f, -2.0f,  1.0f, 1.0f, 0.0f,
    -2.0f,  2.0f, -2.0f,  0.0f, 1.0f, 0.0f,
    -2.0f, -2.0f, -2.0f,  0.0f, 0.0f, 0.0f,

    -2.0f, -2.0f,  2.0f,  0.0f, 0.0f, 1.0f,
    2.0f, -2.0f,  2.0f,  1.0f, 0.0f, 1.0f,
    2.0f,  2.0f,  2.0f,  1.0f, 1.0f, 1.0f,
    2.0f,  2.0f,  2.0f,  1.0f, 1.0f, 1.0f,
    -2.0f,  2.0f,  2.0f,  0.0f, 1.0f, 1.0f,
    -2.0f, -2.0f,  2.0f,  0.0f, 0.0f, 1.0f,

    -2.0f,  2.0f,  2.0f,  0.0f, 1.0f, 1.0f,
    -2.0f,  2.0f, -2.0f,  0.0f, 1.0f, 0.0f,
    -2.0f, -2.0f, -2.0f,  0.0f, 0.0f, 0.0f,
    -2.0f, -2.0f, -2.0f,  0.0f, 0.0f, 0.0f,
    -2.0f, -2.0f,  2.0f,  0.0f, 0.0f, 1.0f,
    -2.0f,  2.0f,  2.0f,  0.0f, 1.0f, 1.0f,

    2.0f,  2.0f,  2.0f,  1.0f, 1.0f, 1.0f,
    2.0f,  2.0f, -2.0f,  1.0f, 1.0f, 0.0f,
    2.0f, -2.0f, -2.0f,  1.0f, 0.0f, 0.0f,
    2.0f, -2.0f, -2.0f,  1.0f, 0.0f, 0.0f,
    2.0f, -2.0f,  2.0f,  1.0f, 0.0f, 1.0f,
    2.0f,  2.0f,  2.0f,  1.0f, 1.0f, 1.0f,

    -2.0f, -2.0f, -2.0f,  0.0f, 0.0f, 0.0f,
    2.0f, -2.0f, -2.0f,  1.0f, 0.0f, 0.0f,
    2.0f, -2.0f,  2.0f,  1.0f, 0.0f, 1.0f,
    2.0f, -2.0f,  2.0f,  1.0f, 0.0f, 1.0f,
    -2.0f, -2.0f,  2.0f,  0.0f, 0.0f, 1.0f,
    -2.0f, -2.0f, -2.0f,  0.0f, 0.0f, 0.0f,

    -2.0f,  2.0f, -2.0f,  0.0f, 1.0f, 0.0f,
    2.0f,  2.0f, -2.0f,  1.0f, 1.0f, 0.0f,
    2.0f,  2.0f,  2.0f,  1.0f, 1.0f, 1.0f,
    2.0f,  2.0f,  2.0f,  1.0f, 1.0f, 1.0f,
    -2.0f,  2.0f,  2.0f,  0.0f, 1.0f, 1.0f,
    -2.0f,  2.0f, -2.0f,  0.0f, 1.0f, 0.0f
};

为了能够显示出3D图形，需要进行坐标变换。需要相应的变换矩阵，实现从局部坐标到世界坐标、从世界坐标到观察坐标、从观察坐标到裁剪坐标的变换。在顶点着色器中添加这些矩阵作为全局变量，再进行矩阵相乘运算后输出，可以实现这个效果。

1
2
3
4
5
6
7
8
9
10
11
12
13
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aColor;

uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;
out vec3 ourColor;

void main() {
    gl_Position = projection * view * model * vec4(aPos, 1.0);
    ourColor = aColor;
}

要完整显示出立方体，要将摄像机向后移动，这个可以通过glm::translate移动场景来创建平移矩阵。要呈现立方体的真实感，需要进行透视投影，可以通过glm::perspective来创建投影矩阵。下面的代码添加在渲染循环过程内。

1
2
3
4
5
6
7
8
9
10
glm::mat4 model = glm::mat4(1.0f);
glm::mat4 view = glm::mat4(1.0f);
glm::mat4 projection = glm::mat4(1.0f);

view = glm::translate(view, glm::vec3(0.0f, 0.0f, -15.0f));
projection = glm::perspective(glm::radians(45.0f), (float)windowWidth / windowHeight, 0.1f, 100.0f);

shader.setMat4("model", model);
shader.setMat4("projection", projection);
shader.setMat4("view", view);

glDisable(GL_DEPTH_TEST)，关闭深度测试，渲染效果如下。这个效果不像是真实的立方体，本该被覆盖的后面被显示了出来。这是因为OpenGL是逐个三角形绘制的，后来绘制的像素有可能会覆盖之前的像素。

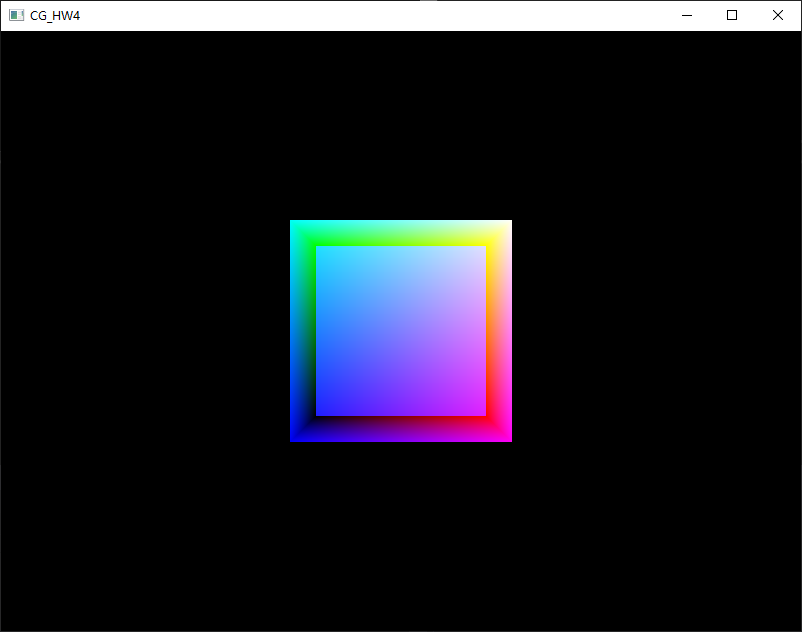
glEnable(GL_DEPTH_TEST) ，启动深度测试，渲染效果如下。这个效果好多了，前面完全覆盖了背面，是一个真实的立方体（虽然这里看上去像正方形）。OpenGL的深度信息存储在Z缓冲中，也叫深度缓冲，GLFW会自动创建这个缓冲。当片段要输出它的颜色时，OpenGL会将它的深度值和z缓冲进行比较，如果当前的片段在其它片段之后，它将会被丢弃，否则将会覆盖。这个过程就是深度测试，由OpenGL自动完成。

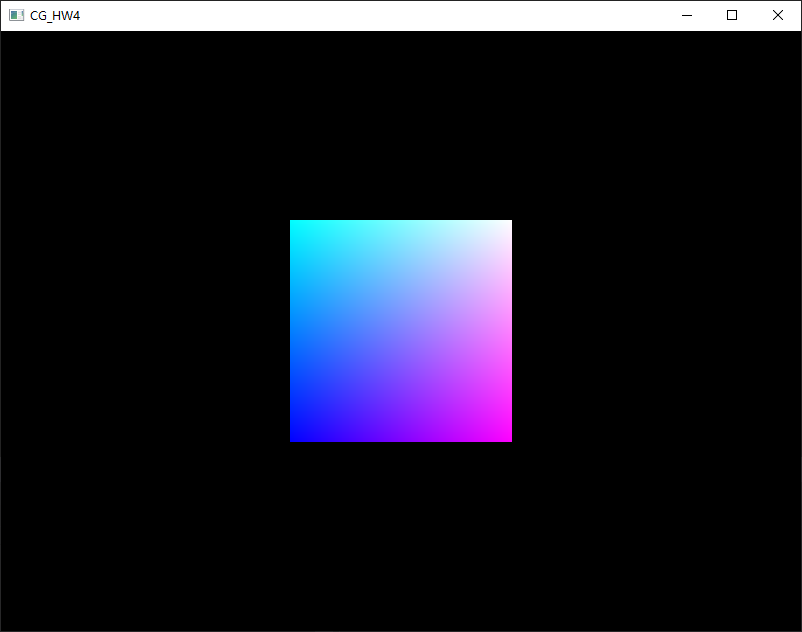
平移(Translation)：使画好的cube沿着水平或垂直方向来回移动

用glm::translate生成平移矩阵，赋给model就可以实现平移。通过三角函数，可以实现立方体沿x轴来回移动。

1
2
float time = (float)glfwGetTime();
model = glm::translate(model, glm::vec3(sin(time) * 4, 0.0f, 0.0f));

效果：

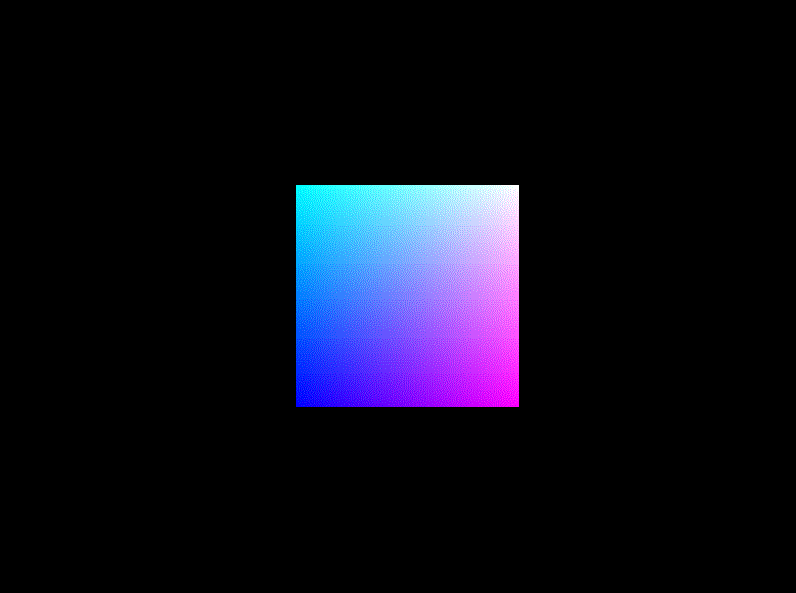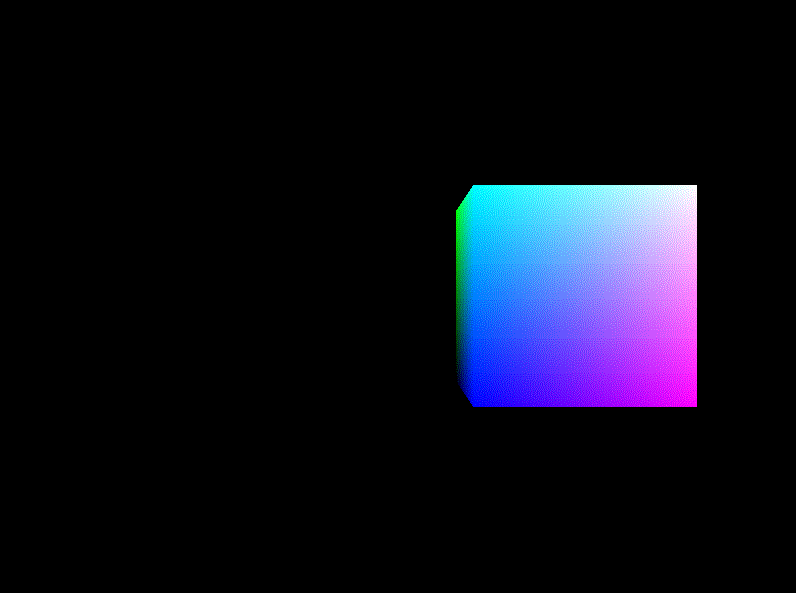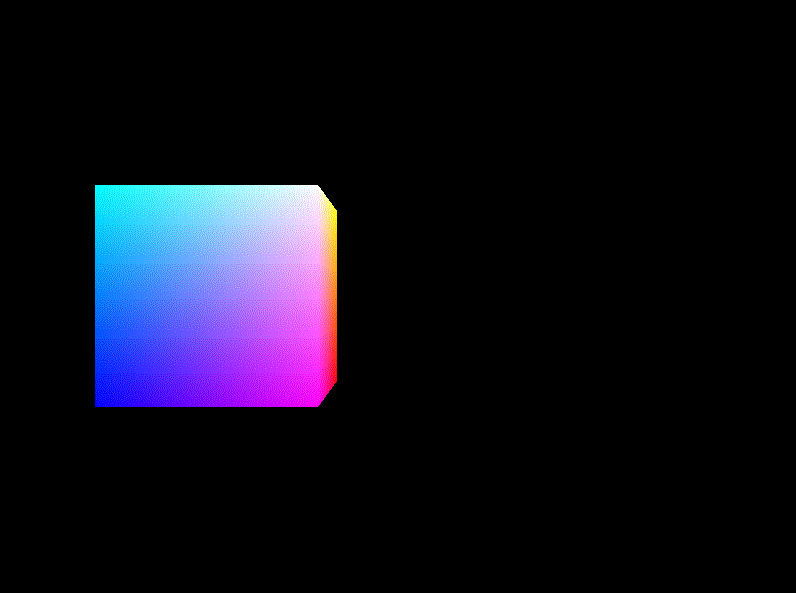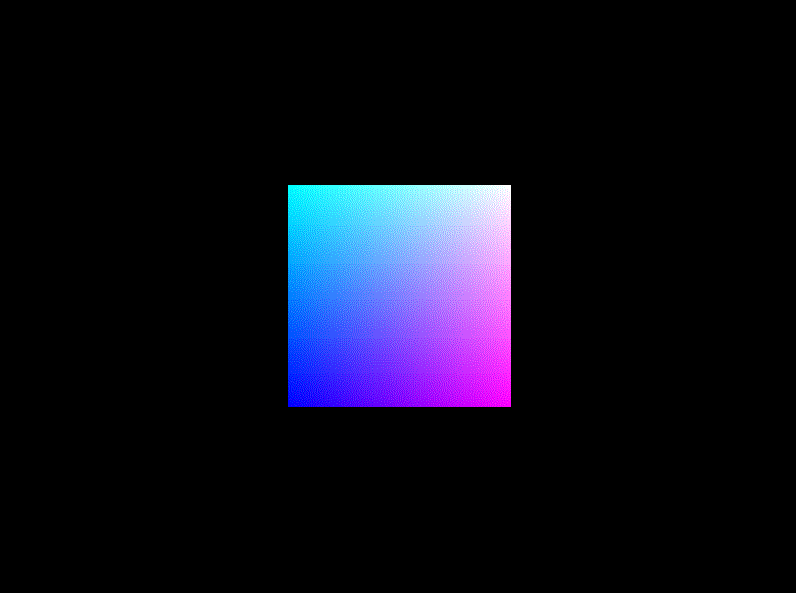
旋转(Rotation)：使画好的cube沿着XoZ平面的x=z轴持续旋转

用glm::rotate生成旋转矩阵，赋给model就可以实现旋转。坐标设置为(1, 0, 1)，可以沿着x=z轴旋转。

1
2
float time = (float)glfwGetTime();
model = glm::rotate(model, time * 2 * glm::radians(50.0f), glm::vec3(1.0f, 0.0f, 1.0f));

效果：

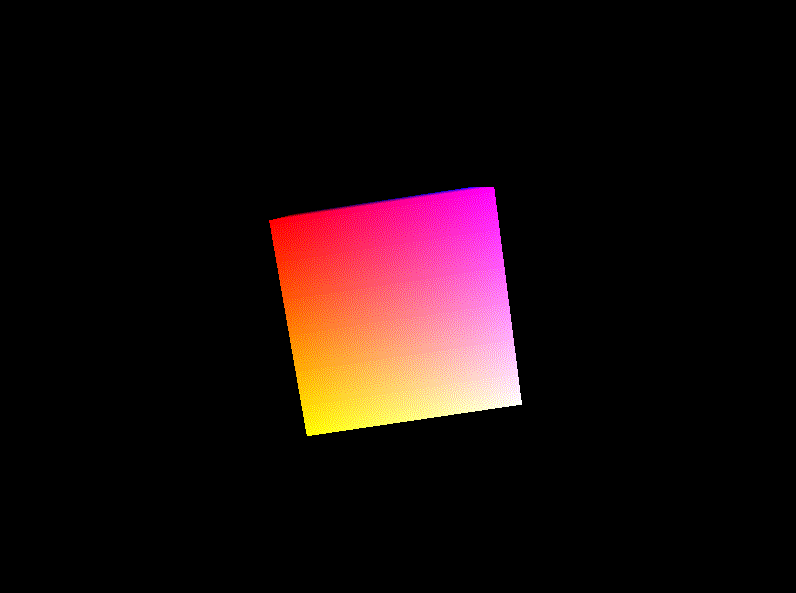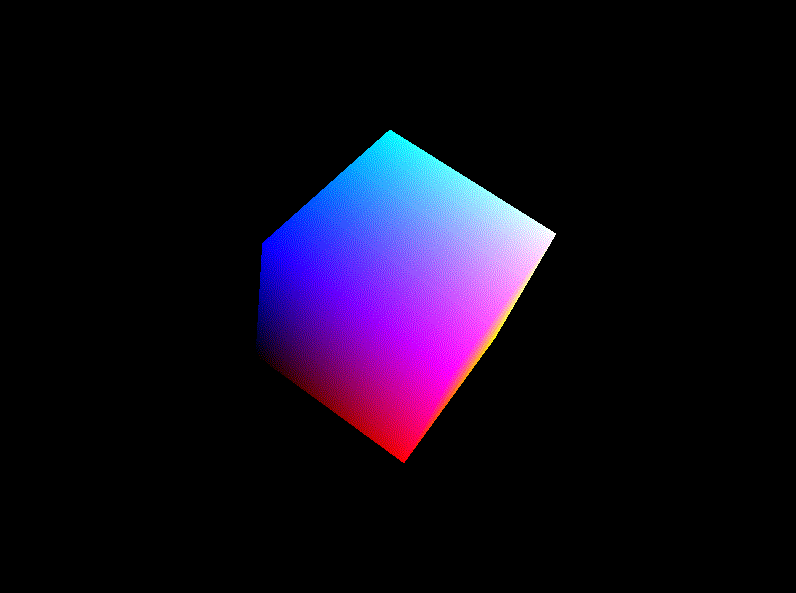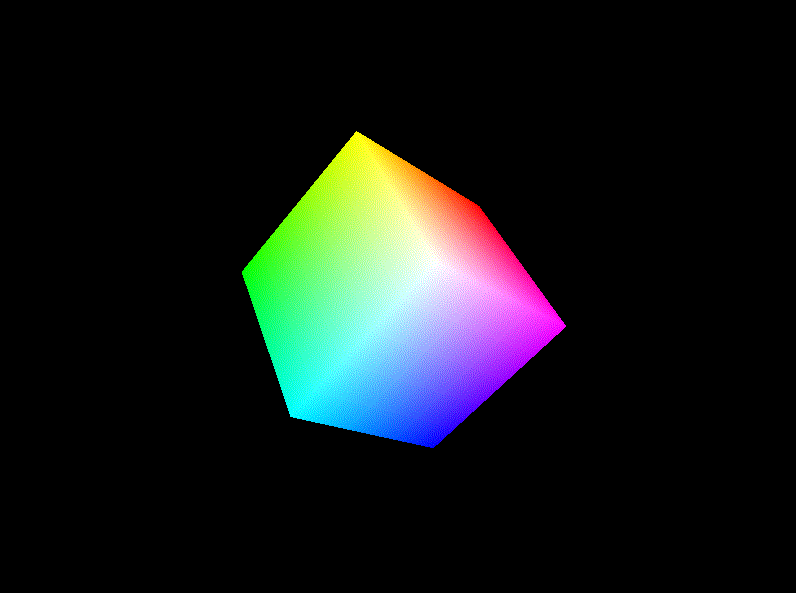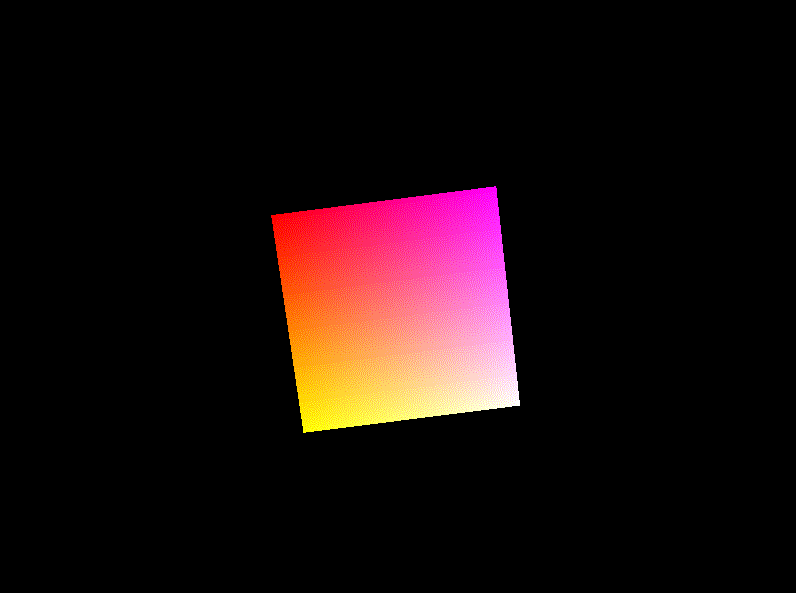
放缩(Scaling)：使画好的cube持续放大缩小

用glm::scale生成放缩矩阵，赋给model就可以实现放缩。利用三角函数和时间可以实现持续放缩。

1
2
float time = (float)glfwGetTime();
model = glm::scale(model, glm::vec3(0.5 * sin(time) + 1, 0.5 * sin(time) + 1, 0.5 * sin(time) + 1));

效果：

在GUI里添加菜单栏，可以选择各种变换

用GUI将上述变换整合起来，得到结合的变换。旋转变换一定要放在最后，否则会使立方体偏离位置。

1
2
3
4
5
6
7
8
9
10
11
12
if (ImGui::MenuItem("translate", NULL, &translate))
    translateTime = (float)glfwGetTime();
if (ImGui::MenuItem("scale", NULL, &scale))
    scaleTime = (float)glfwGetTime();
if (ImGui::MenuItem("rotate", NULL, &rotate))
    rotateTime = (float)glfwGetTime();
if (translate)
    model = glm::translate(model, glm::vec3(sin( (time - translateTime)) * 4, 0.0f, 0.0f));
if (scale)
    model = glm::scale(model, glm::vec3(0.5 * sin(time - scaleTime) + 1, 0.5 * sin(time - scaleTime) + 1, 0.5 * sin(time - scaleTime) + 1));
if (rotate)
    model = glm::rotate(model, (time - rotateTime) * 2 * glm::radians(50.0f), glm::vec3(1.0f, 0.0f, 1.0f));

效果：

结合Shader谈谈对渲染管线的理解

渲染管线的作用是接受3D坐标，最终将它们转变成屏幕上的有色2D像素。渲染管线可以被划分成几个阶段，这些阶段高度专门化，并且容易并行执行。这些阶段在显卡中有各自对应的小程序，这些小程序就是着色器（Shader）。

渲染管线的第一个阶段是顶点着色器，它接受一个顶点坐标作为输入，进行坐标变换，处理顶点属性，然后输出变换后的3D坐标和属性。下一个阶段是图元装配，根据图元的类型接受来自顶点着色器的输入，将这些输入的坐标组装成对应的图元形状。几何着色器是第三个阶段，接受来自图元装配阶段的输入，通过产生新的顶点，构造新的图元，产生其他形状的图形。之后，数据会传入光栅化阶段，这个阶段会将图元映射到屏幕空间，生成片段，并且会裁剪出视口以外的像素。下一个阶段是片段着色器，能够计算像素的颜色，用于光照、阴影、颜色等效果。最后是Alpha测试和混合阶段，这个阶段进行深度检测和Alpha值检测，能够判断物体的深度和透明度，实现对象的遮挡和混合，最终输出符合预期的渲染效果。

Bonus: 将以上三种变换相结合，打开你们的脑洞，实现有创意的动画。

将平移和旋转结合起来，实现立方体在水平面上的滚动动画。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
if (flip) {
    // 判断旋转周期
    if (time - flipTime > 1) {
        std::cout << time - flipTime << std::endl;
        flipTime = time;
        cycle++;
        shift += 4;
    }

    // 在不同的旋转周期，实现不同的变换
    model = glm::translate(model, glm::vec3((shift + 2 - 20), -2.0f, 0.0f));
    model = glm::rotate(model, - (time - flipTime) * glm::radians(90.0f), glm::vec3(0.0f, 0.0f, 1.0f));
    model = glm::translate(model, glm::vec3(-2.0f, 2.0f, 0.0f));
    model = glm::rotate(model, -(cycle - 1) * glm::radians(90.0f), glm::vec3(0.0f, 0.0f, 1.0f));
}

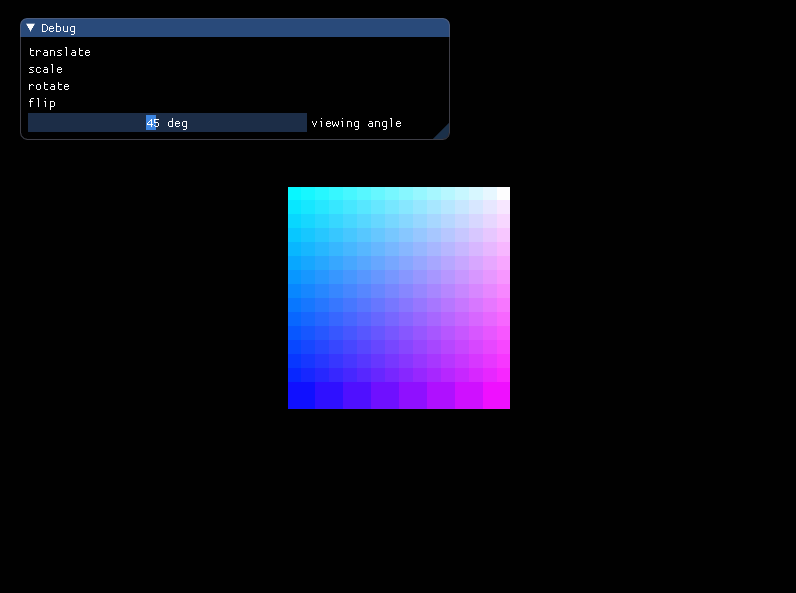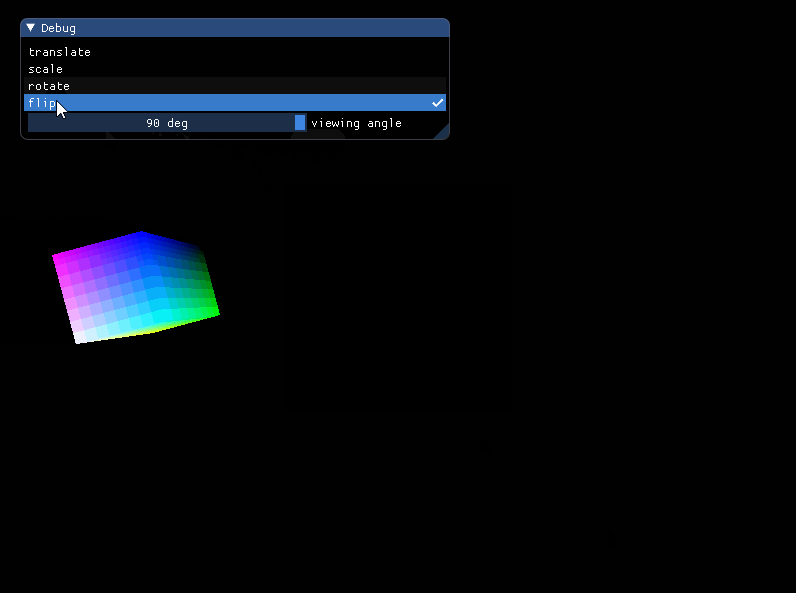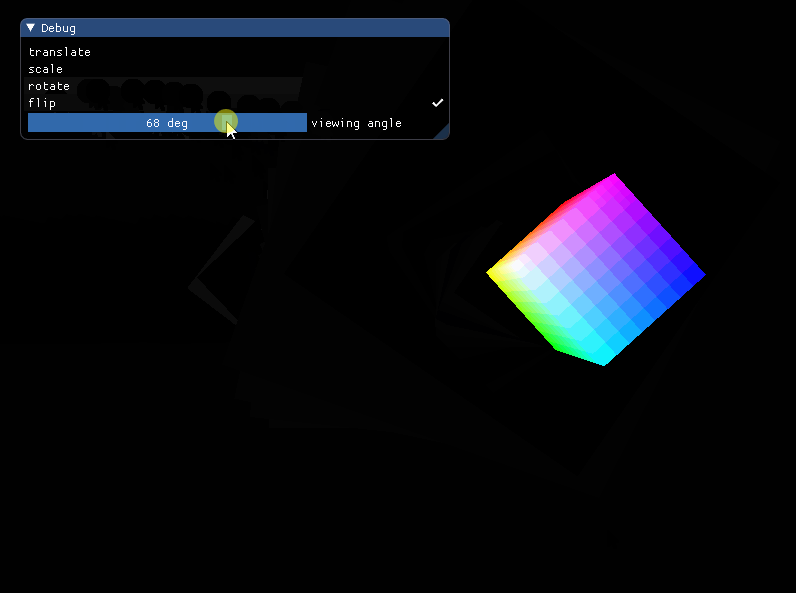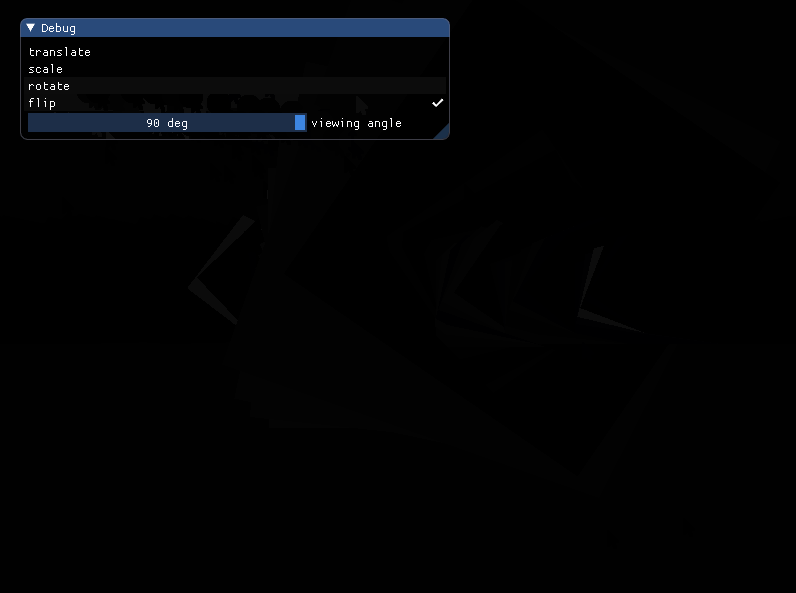
此外，通过滑块调整投射投影的可视角度，能够方便地调节场景可视范围。

1
2
ImGui::SliderAngle("viewing angle", &viewAngle, 10, 90);
projection = glm::perspective(viewAngle, (float)windowWidth / windowHeight, 0.1f, 100.0f);

效果：

CATALOG
  1. 1. 画一个立方体，边长为4，中心位置为(0, 0, 0)
  2. 2. 平移(Translation)：使画好的cube沿着水平或垂直方向来回移动
  3. 3. 旋转(Rotation)：使画好的cube沿着XoZ平面的x=z轴持续旋转
  4. 4. 放缩(Scaling)：使画好的cube持续放大缩小
  5. 5. 在GUI里添加菜单栏，可以选择各种变换
  6. 6. 结合Shader谈谈对渲染管线的理解
  7. 7. Bonus: 将以上三种变换相结合，打开你们的脑洞，实现有创意的动画。
Total : 43
2020
2019
2018
2017
Android Computer Graphics iOS UWP Unity Java Linux 实训 blog Face-Recognition Image-Understanding Azure Computer Vision SE
Unity